Excel 数値の調和平均を取得(HARMEAN関数)
HARMEAN関数は指定セル範囲の数値の調和平均を取得する関数です。
この記事では関数の仕様と使い方、調和平均の初歩的な説明、
AVERAGE関数(算術平均)との違いを紹介します。
仕様
=HARMEAN(数値1~255)
| 引数 | 省略時の値 | 説明 |
|---|---|---|
| 数値1~255 | 省略不可 | 調和平均する数値を指定。 |
使い方と調和平均について
調和平均の用途は様々ですが、一般的な領域では
一定の距離を幾つかの速度で移動した場合の平均に用います。
例えば家と会社を往復する場合、「行きの速度」を時速0.5Km、
「帰りの速度」を時速0.25Kmとします。
(計算を単純にしたいので、現実的に遅すぎなのはスルーしてください)
この二つの速度に対してAVERAGE関数(算術平均)を出すと時速0.38Kmになり、
HARMEAN関数(調和平均)では時速0.33Kmになります。
| 項目 | 値 | 単位 |
|---|---|---|
| 行きの速度 | 0.50 | km/時 |
| 帰りの速度 | 0.25 | km/時 |
| 算術平均の速度 | 0.38 | km/時 |
| 調和平均の速度 | 0.33 | km/時 |
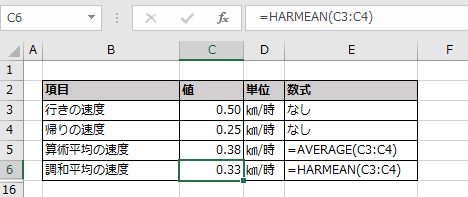
単純に速さの平均だけであれば算術平均で構いませんが、
一定の距離を往復した場合、その往復の平均移動速度を出す場合は
算術平均ではなく調和平均の速度が正解になります。
なぜなら遅い方の速度で移動している時間が長くなるため、
行きと帰りの速度の重みが異なるためです。
例えば片道1Kmの道を往復すると場合に、
行きが2時間になり、帰りが4時間になります。
| 項目 | 値 | 単位 |
|---|---|---|
| 片道の距離 | 1 | km |
| 行きの移動時間 | 2 | 時間 |
| 帰りの移動時間 | 4 | 時間 |
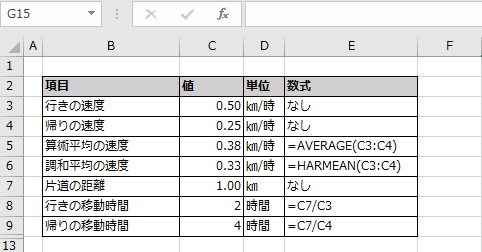
往復の距離は1Kmの2倍で2Km、往復の時間は行き2時間+帰り4の6時間になります。
往復の距離を往復時間を割ると往復速度になり、
それを計算すると調和平均の結果と同じ0.33になります。
| 項目 | 値 | 単位 |
|---|---|---|
| 往復の時間 | 6 | 時間 |
| 往復の距離 | 2 | km |
| 往復の移動速度 | 0.33 | km/時 |
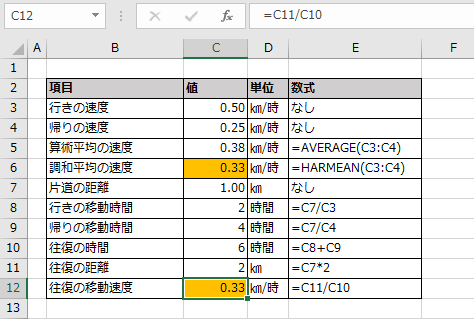
このように同じ距離を異なる速度で移動する場合は、
算術平均でなく調和平均で算出するのが正解になります。
計算式(算術平均と調和平均)
値が何個あるかをNと表現し、それぞれの計算式は以下のようになります。
マーカーは()で囲まれるなど、数式のまとまりを表現しています。
| 算術平均(AVERAGE) | (値1 + 値2 + …省略… + 値N) ÷ N |
| 調和平均(HARMEAN) | N ÷ ( (1÷値1) + (1÷値2) + …省略… + (1÷値N) ) |
Excelを効率的に習得したい方へ
当サイトの情報を電子書籍用に読み易く整理したコンテンツを
買い切り950円またはKindle Unlimited (読み放題) で提供中です。

Word-A4サイズ:1,400ページの情報量で
(実際のページ数はデバイスで変わります)
基本的な使い方、関数の解説(140種類)、
頻出テクニックと実用例(109種類)、
XLOOKUP関数、LET関数、シートビュー、LAMBDA関数、スピルなど便利な新機能を紹介。
体系的に学びたい方は是非ご検討ください。
アップデートなどの更新事項があれば随時反映しています。
なお購入後に最新版をダウンロードするには
Amazonへの問い合わせが必要です。