Excel 数値の幾何平均(相乗平均)を取得(GEOMEAN関数)
GEOMEAN関数は指定セル範囲の数値の幾何平均(相乗平均)を取得する関数です。
この記事では関数の仕様と使い方、幾何平均(相乗平均)の初歩的な説明、
AVERAGE関数(算術平均)との違いを紹介します。
仕様
=GEOMEAN(数値1~255)
| 引数 | 省略時の値 | 説明 |
|---|---|---|
| 数値1~255 | 省略不可 | 幾何平均(相乗平均)する数値を指定。 |
使い方と幾何平均(相乗平均)について
幾何平均(相乗平均)の用途は様々ですが、
一般的な領域では成長率や変動する利率の平均に用います。
(例えば数年の率を1年に均した率)
例えば下の表のようにB列に年度、1年ごとの売上高、
D列に変化率(当年売上高 ÷ 前年売上高)を出します。
この変化率から100%を引くと成長率になります。
負の数が混ざるとGEOMEAN関数がエラーなるため、
通常の使い方では正の数にしかならない変化率を計算に使用します。
(2018年度が極端に低いですが説明のためです)
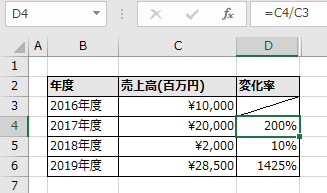
2017年度から2019年度の変化率の平均を出します。
GEOMEAN関数もAVERAGE関数(算術平均)と同じ使い方です。

初年度(2016年度)の売上高に算術平均(E列)と幾何平均(F列)を掛けていきます。
すると幾何平均の計算結果が最終年度の2019年度の売上高と一致します。
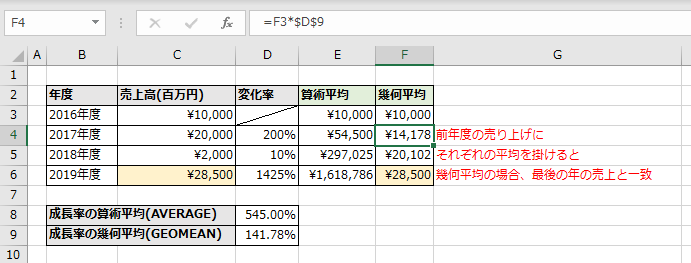
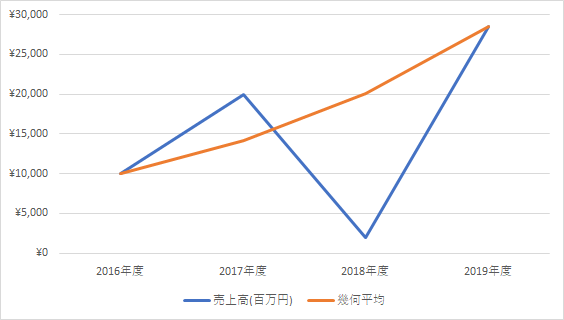
これにより2019年までの変化率(100%を引けば成長率)を
1年あたりの変化率を出す場合、幾何平均の方が適切であることがわかります。
(年ではなく月や日でも同じく利用可能です)
計算式(算術平均と幾何平均)
値が何個あるかをNと表現し、それぞれの計算式は以下のようになります。
マーカーは()で囲まれるなど、数式のまとまりを表現しています。
| 算術平均(AVERAGE) | (値1 + 値2 + …省略… + 値N) ÷ N |
| 幾何平均(GEOMEAN) | N乗根(値1 × 値2 × …省略… × 値N) |
N乗根はN乗の逆です。(平方根は2乗の逆)
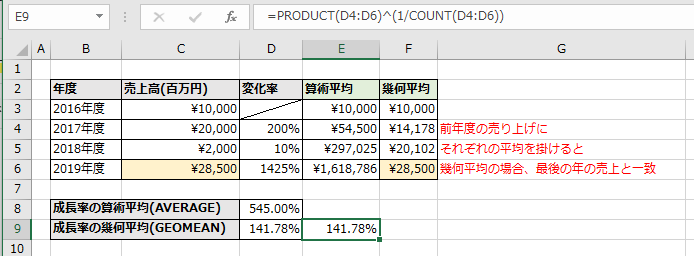
^(べき乗演算子)を使って1/N(NはCOUNT関数、値の掛け算はPRODUCT関数を使用)と
計算すればGEOMEAN関数と同じ結果になります。(E9セル)
Excelを効率的に習得したい方へ
当サイトの情報を電子書籍用に読み易く整理したコンテンツを
買い切り950円またはKindle Unlimited (読み放題) で提供中です。

Word-A4サイズ:1,400ページの情報量で
(実際のページ数はデバイスで変わります)
基本的な使い方、関数の解説(140種類)、
頻出テクニックと実用例(109種類)、
XLOOKUP関数、LET関数、シートビュー、LAMBDA関数、スピルなど便利な新機能を紹介。
体系的に学びたい方は是非ご検討ください。
アップデートなどの更新事項があれば随時反映しています。
なお購入後に最新版をダウンロードするには
Amazonへの問い合わせが必要です。