Excel 標準偏差を取得(STDEV.P関数)
標準偏差とはデータの散らばり具合を示す数値です。
標準偏差の関数には二つありますが、
今回は全数検査のSTDEV.P関数を用います。
(STDEV.S関数は抜き取り検査)
その基本的な使用と使い方を紹介します。
仕様
関数の使用方法はSUM関数など基本的な集計関数と変わりありません。
=STDEV.P関数(数値)
| 引数 | 省略時の値 | 説明 |
|---|---|---|
| 数値 | 省略不可 | 標準偏差を取得するセル範囲を指定。 |
標準偏差の値
標準偏差は数式や文章での説明ではイメージが掴み辛い方が多いと
思われるので単純な例を示します。
8行目に縦に5セル並んだデータがあり
値はそれぞれ違いますが、平均は50で共通しています。
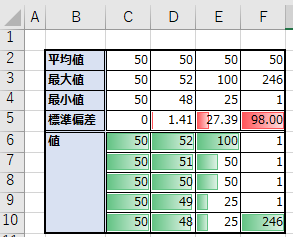
まずC8~10は全ての値が50です。
全てが平均と同一の値の場合、標準偏差は0、バラつきなしとなります。
D8~10は48~52の値になっており、平均値より少し離れた値が出てくるため
標準偏差が1.41となっています。そしてE、Fは更にバラつきが大きくなります。
活用例(データの性質を把握・数値予測のための参考)
統計学なにそれ美味しいの?な私でも扱える単純な方法だと
主にデータの性質を把握したり、
「1月と2月」や、「月曜日と火曜日」のような複数系列の比較で用います。
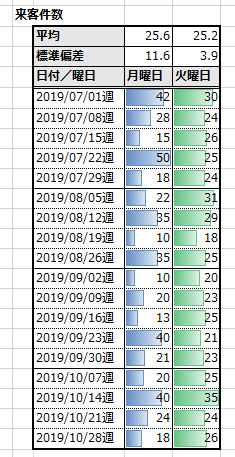
この例だと月曜日と火曜日の来客件数に平均と標準偏差を出しています。
結果の比較すると月曜日の方がバラつきが多く、火曜日は少ないことが分かります。
この程度の数量だとざっくり感覚で分かるかもしれませんが、
数量が多くなるとそうはいきません。また定量比較可能なところも大きいです。
(本格的になるともっと色々やりますが)
また標準偏差と平均があると未来の来客数を見積もる目安となります。
- 平均-(標準偏差×1)から平均+(標準偏差×1)となる確率が約68%
- 平均-(標準偏差×2)から平均+(標準偏差×2)となる確率が約95%
- それ以外が約5%(突き詰めるともっと細かいですが)
ざっくり計算でこのような感じです。
| 月曜日 | 14~37の間となる確率が約68% 2~48の間となる確率が約95% |
| 火曜日 | 21~29となる確率が約68% 17~33となる確率が約95% |
正規分布という人間、自然、社会はそういう風になりやすいというモデルがあり
それと同様と仮定しているだけで、実際にそうなるかは別ですが、
何も基準なしに考えるよりは有意義です。
この標準偏差に更に最大値(MAX関数)、最小値(MIN関数)、中央値(MEDIAN関数)、
場合によって最頻値やヒストグラムを併用すると更にデータの性質が見えてきます。
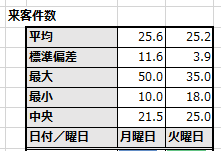
これ以降どうするかは、より高度な手法を使うか「経験と勘と度胸」になってしまいますが
結局、このあたりの算出値は「過去の傾向としてそうなりやすかった」だけで
ずっとそうだと決まるわけでないため未来を予知できるわけではありません。
天気、気温、社会情勢などなど様々な変動要素があります。
しかし平均値だけで考えるよりは論理的な判断材料となることは間違いありません。
Excelを効率的に習得したい方へ
当サイトの情報を電子書籍用に読み易く整理したコンテンツを
買い切り950円またはKindle Unlimited (読み放題) で提供中です。

Word-A4サイズ:1,400ページの情報量で
(実際のページ数はデバイスで変わります)
基本的な使い方、関数の解説(140種類)、
頻出テクニックと実用例(109種類)、
XLOOKUP関数、LET関数、シートビュー、LAMBDA関数、スピルなど便利な新機能を紹介。
体系的に学びたい方は是非ご検討ください。
アップデートなどの更新事項があれば随時反映しています。
なお購入後に最新版をダウンロードするには
Amazonへの問い合わせが必要です。